Cuáles son los números primos y compuestos: definiciones, ejemplos, tabla de números primos, criba de Eratóstenes

El artículo analiza los conceptos de números primos y compuestos. Las definiciones de dichos números se dan con ejemplos. Presentamos una prueba de que el número de números primos es ilimitado y lo registraremos en la tabla de números primos utilizando el método de Eratóstenes. Se dará evidencia para determinar si un número es primo o compuesto.

Números primos y compuestos: definiciones y ejemplos

Los números primos y compuestos se clasifican como números enteros positivos. Deben ser mayores que uno. Los divisores también se dividen en simples y compuestos. Para comprender el concepto de números compuestos, primero debes estudiar los conceptos de divisores y múltiplos.

Definición 1: Los números primos son números enteros mayores que uno y que tienen dos divisores positivos, es decir, ellos mismos y 1.

Definición 2: Los números compuestos son números enteros mayores que uno y que tienen al menos tres divisores positivos.

Uno no es un número primo ni compuesto. Tiene un solo divisor positivo, por lo que es diferente de todos los demás números positivos. Todos los números enteros positivos se llaman números naturales, es decir, se utilizan para contar.

Definición 3: Los números primos son números naturales que tienen sólo dos factores positivos.

Definición 4: Un número compuesto es un número natural que tiene más de dos factores positivos.

Cualquier número que sea mayor 1 es simple o compuesto. De la propiedad de divisibilidad tenemos que 1 y el numero a siempre sera divisor de cualquier numero A, es decir, se dividirá en sí mismo y en 1. Demos una definición de números enteros.

Definición 5: Los números naturales que no son primos se llaman números compuestos.

Números primos: 2, 3, 11, 17, 131, 523. Están divididos sólo en ellos mismos y 1.

Números compuestos: 6, 63, 121, 6697. Es decir, el número 6 se puede descomponer en 2 y 3, A 63 en 1, 3, 7, 9, 21, 63, a 121 en 11, es decir, sus divisores serán 1, 11 y 121.

Tenga en cuenta que los conceptos de números primos y números coprimos son conceptos diferentes.

Tabla de números primos

Para facilitar el uso de números primos, es necesario utilizar una tabla:

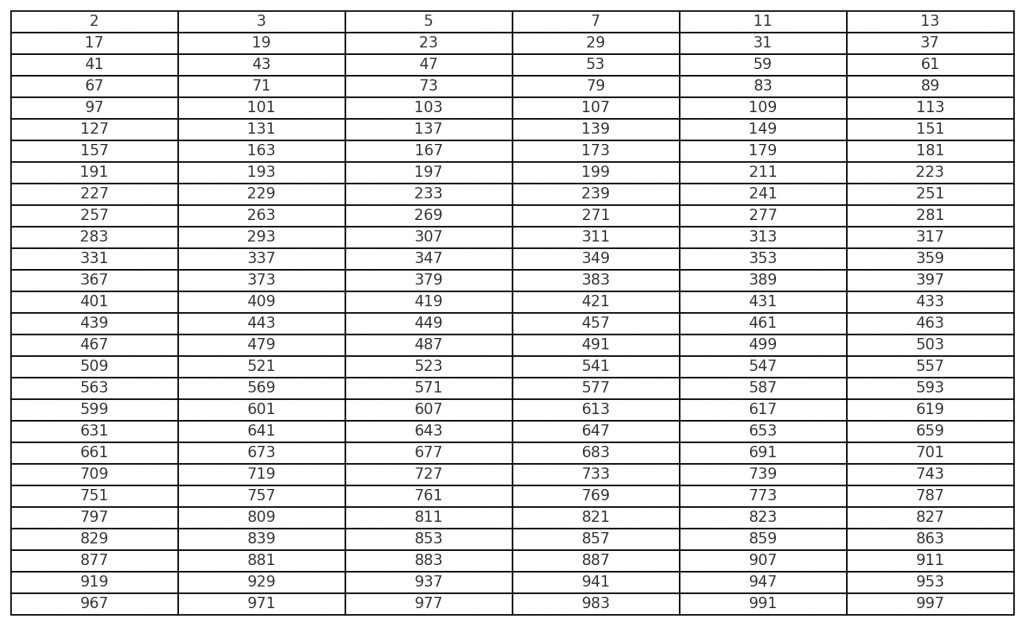
Una tabla para todos los números naturales existentes no es realista, ya que hay un número infinito de ellos. Cuando los números se hacen grandes 10000 o 1000000000, entonces deberías pensar en utilizar el tamiz de Eratóstenes.

Consideremos el teorema que explica el último enunciado.

Teorema 1: Menos positivo y diferente de 1 El divisor de un número natural mayor que uno es un número primo.

Evidencia 1: Supongamos que A es un número natural mayor 1, B es el divisor distinto de uno más pequeño del número A . Se debe demostrar que B es un número primo usando el método de adversación.

Supongamos que B es un número compuesto. De aquí tenemos que hay un divisor para B, que es diferente de 1 así como de B. Tal divisor se denota como B1. Es necesario que la condición 1 < b1 < b sea correcta.

De la condición se desprende claramente que A dividido por b , dividido por b₁, lo que significa que el concepto de divisibilidad se expresa de la siguiente manera: a=b⋅q Y b = b₁⋅q₁, dónde a= b1⋅(q1⋅q), Dónde q Y q₁ son números enteros. Según la regla de multiplicación de números enteros, tenemos que el producto de números enteros es un número entero con igualdad de la forma a=b1⋅(q1⋅q). Está claro que b₁ es el divisor del numero A. Desigualdad 1 < b₁ <b no corresponde, porque entendemos eso b es el menos positivo y diferente de11divisorAа.Teorema 2

Hay una cantidad infinita de números primos.

Tamiz de Eratóstenes

Al compilar una tabla de números primos, se debe tener en cuenta que dicha tarea requiere una verificación secuencial de números, comenzando con22antes100100. Si no hay divisor, se registra en la tabla; si es compuesto, entonces no se ingresa en la tabla.

Veámoslo paso a paso.

Si empiezas con el número 2, entonces solo tiene 2 divisores: 2 y 1, lo que significa que se puede ingresar en la tabla. Lo mismo con los números 3. Número 4 es compuesto, debe descomponerse aún más en 2 y 2. Número 5 es simple, lo que significa que se puede registrar en una tabla. Haga esto hasta que el número 100.

Este método es inconveniente y requiere mucho tiempo. Es posible crear una tabla, pero tendrás que dedicar mucho tiempo. Es necesario utilizar criterios de divisibilidad, lo que acelerará el proceso de encontrar divisores.

El método que utiliza el tamiz de Eratóstenes se considera el más conveniente. Veamos las tablas siguientes como ejemplo. Primero, escribe los números.2, 3, 4, …, 50.

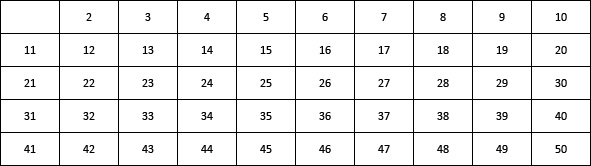
Ahora necesitas tachar todos los números que son múltiplos de 2. Realizar tachados secuenciales. Obtenemos una tabla como:

A continuación, tacha todos los números que sean múltiplos de 3. Obtenemos una tabla como:

Pasemos a tachar números que son múltiplos de 5. Obtenemos:

Tachar múltiplos de números 7 y 11. Al final la mesa parece:

Pasemos a la formulación del teorema.

¿Este número es primo o compuesto?

Antes de resolver, debes averiguar si el número es primo o compuesto. A menudo se utilizan criterios de divisibilidad. Veamos esto en el siguiente ejemplo.

Ejemplo 1: Demuestre que el número 8989898989898989 es compuesto.

Solución

La suma de las cifras de un número dado es igual a 9⋅8 + 9⋅9 = 9⋅17. entonces el numero 9⋅17 dividido por 9, basado en la prueba de divisibilidad por 9. De ello se deduce que es compuesto.

Estos signos no pueden demostrar la primacía de un número. Si se necesita verificación, se deben tomar otras acciones. La forma más adecuada es enumerar números. Durante el proceso se pueden encontrar números primos y compuestos. Es decir, los números no deben exceder en valor.√a. Es decir, el número a debe descomponerse en factores primos. si esto se cumple, entonces el número a puede considerarse primo.

Ejemplo 2: Identificar un número compuesto o primo 11723.

Solución

Ahora necesitas encontrar todos los divisores del número 11723. Necesita ser evaluado √11723.

Para una estimación más precisa del número √11723 necesitas escribir la expresión 108² = 11664, 109²=11881. Por tanto 108² < 11 723 < 109². Resulta que √11723 <109. Se puede observar que cualquier número menor de 109 se considera divisor de un número dado.

Al expandirnos conseguimos que 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107… todos estos son números primos. Todo este proceso se puede representar como una división por una columna. Es decir, dividir 11723 en 19. Número 19 es uno de sus factores, ya que obtenemos la división sin resto. Representemos la división como una columna:

Respuesta: Resulta que 11723 es un número compuesto, porque además de sí mismo y 1 tiene como divisor el 19.